When manufacturers release vehicle specifications, it’s important to understand that these figures serve a dual purpose: to inform potential buyers and, ultimately, to sell vehicles. Navigating these specifications can be complex, especially when comparing vehicles with different units of measurement. For instance, understanding the difference between horsepower (hp) and kilowatt (kW) for engine power can be confusing depending on your familiarity with either metric.
To truly understand vehicle performance, particularly when comparing a high-performance SUV like the Lamborghini Urus – which we can consider a “Lamborghini Truck” in the context of its SUV body style – to a more traditional truck, we need to delve deeper than just the headline numbers. Let’s break down the key factors that contribute to acceleration and overall performance.
The fundamental principle governing a vehicle’s acceleration ($a$) is Newton’s second law of motion: Force ($F$) equals mass ($m$) times acceleration ($a$), or $F = ma$. The greater the force applied to the vehicle through tire-ground contact, and the lower the vehicle’s mass, the quicker it will accelerate.
Engine power ($P$) and torque ($tau$) are crucial specifications, typically provided as maximum values achieved at specific engine speeds. These are related by the equation $P = tau omega$, where $omega$ is the engine’s angular speed. Understanding these characteristics is vital for comparing different vehicles.
Let’s consider a comparison between a Lamborghini and a Ford truck to illustrate these points. The following graphs represent the power and torque curves for a Lamborghini engine, and a representative engine you might find in a Ford truck. Note that these are generalized representations due to variations across different engine types and model years.
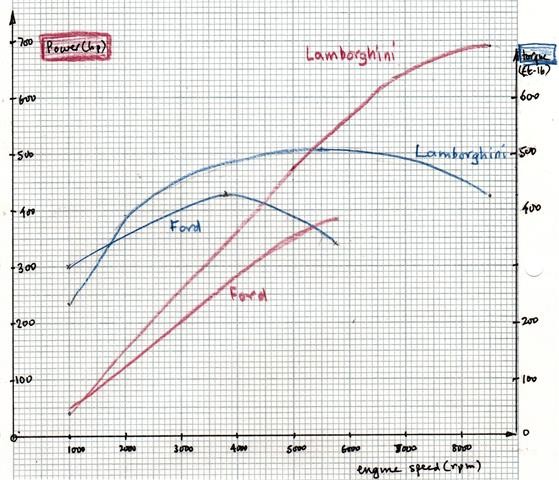Engine Power and Torque Curves Comparison
Alt text: A graph comparing engine power and torque curves between a Lamborghini (solid line) and a Ford truck (dashed line), showing higher peak power and torque at different engine speeds and ranges.
As the graph indicates, the Lamborghini engine is designed to reach a higher maximum engine speed compared to a typical truck engine. Crucially, the mass of the vehicles plays a significant role. The Lamborghini Urus, with a lighter mass (around 1690 kg, depending on the specific model), is considerably lighter than a Ford truck (which can be around 2745 kg or more). This weight difference means that for the same amount of force applied, the Lamborghini will experience significantly greater acceleration.
However, the torque generated by the engine isn’t directly transferred to the wheels. It’s modified through the drivetrain, starting with the gear ratios within the transmission and the final drive ratio in the differential. Gear ratios are designed to reduce the rotational speed and increase the torque delivered to the wheels. To achieve maximum torque at the wheels for initial acceleration, lower gears with higher gear ratios are used.
Let’s examine the gear ratios of a Lamborghini and a Ford truck to see how they compare in torque multiplication:
Lamborghini Gear Ratios (7-speed transmission):
- 1st: 3.91:1
- 2nd: 2.44:1
- 3rd: 1.81:1
- 4th: 1.46:1
- 5th: 1.19:1
- 6th: 0.97:1
- 7th: 0.84:1
- Differential Ratio: 3.54:1
In first gear, the total torque multiplication for the Lamborghini is approximately $3.91 times 3.54 approx 13.8$, assuming some drivetrain losses.
Ford Truck Gear Ratios (6-speed transmission):
- 1st: 3.97:1
- 2nd: 2.31:1
- 3rd: 1.51:1
- 4th: 1.14:1
- 5th: 0.85:1
- 6th: 0.67:1
- Differential Ratio: 3.73:1
In first gear, the Ford truck has a torque multiplication of roughly $3.97 times 3.73 approx 14.8$, which is slightly higher than the Lamborghini in this simplified comparison. Furthermore, some Ford truck variants, especially diesel models, can produce significantly higher torque at lower RPMs. For example, a turbo-diesel Ford truck might have a maximum torque of 925 ft-lb at 1800 rpm, with a first gear ratio of 4.17:1 and a differential ratio of 4.10:1, resulting in even greater torque at the wheels in lower gears.
The final piece of the puzzle is the wheel radius ($R$). The torque at the wheels is related to the accelerating force by:
Torque at wheels = Accelerating force $times$ Radius of wheels
The Lamborghini Urus, being a four-wheel-drive vehicle, typically uses performance tires with specifications like front tyres 335/30YR20 and rear tyres 255/35YR19. Converting these specifications, the approximate wheel radii are around 14 inches for the front and 13 inches for the rear.
Ford trucks, designed for different purposes, often have larger wheel radii. For instance, a tire designation of 265/75R16 translates to a radius of approximately 15.8 inches. A larger wheel radius means that for a given torque at the wheels, the accelerating force is reduced.
Considering all these factors – engine power and torque characteristics, gear ratios, vehicle mass, and wheel radius – the Lamborghini Urus achieves superior acceleration primarily due to its significantly lower mass compared to a Ford truck. Even though a diesel Ford truck might deliver comparable or even higher torque, the weight disadvantage and larger wheel radius hinder its acceleration capabilities relative to the lighter, performance-oriented Lamborghini “truck”.
Once vehicles are in motion, aerodynamic drag forces become increasingly important, especially at higher speeds. Drag force ($F_{rm drag}$) is approximated by $F_{rm drag} = frac 12 c_D A rho v^2$, where $c_D$ is the drag coefficient, $A$ is the frontal area, $rho$ is the air density, and $v$ is the vehicle speed.
Manufacturers specify drag coefficients, and the Lamborghini Urus boasts a significantly lower drag coefficient (around 0.23) compared to a Ford truck (around 0.4). Additionally, the frontal area ($A$) of a Ford truck is considerably larger (around $8, rm m^2$) than that of the Lamborghini Urus (around $2.3, rm m^2$).
At maximum speed, the power delivered by the engine equals the power required to overcome drag and other frictional forces. With its higher power output, lower drag coefficient, and smaller frontal area, the Lamborghini Urus achieves a much higher top speed (around 217 mph) compared to most Ford trucks, although modified Ford trucks have been known to reach impressive speeds.
In conclusion, the fundamental difference between a “Lamborghini truck” like the Urus and a traditional Ford truck lies in their intended usage. Ford trucks prioritize torque for hauling and towing heavy loads, achieved through optimized gear ratios that amplify engine torque. However, their engine speed is relatively lower, and gearing is spaced to allow for a reasonable top speed. Lamborghini, on the other hand, prioritizes speed and performance. The gearing in the Urus is designed to keep the engine operating near its maximum power output across a wide range of speeds. While Lamborghini has continuously increased maximum power by raising maximum engine speeds over the years, the focus on maximizing torque has been less pronounced, reflecting its performance-oriented design philosophy.
